小雪第一次尝到又大又粗,女仆穿白丝裸体吃奶玩乳视频,乖宝撞的你舒不舒服H,无码人妻熟妇AV又粗又大

本文由銅陵市工業學校的蘇文忠老師供稿

我們經常會看到鏤空裝飾球體的模型，在用三維軟件建模時，曲面模型的控制不太容易，往往會使球表面圖案變形，出現中間正常，兩端變小等現象。如何使球表面圖案的大小等大呢？根據歐拉定律,簡單正多面體只有五種: 正四面體、正六面體、正八面體、正十二面體和正二十面體，今天我們以這五個正多面體分別來探討下其中的規律。

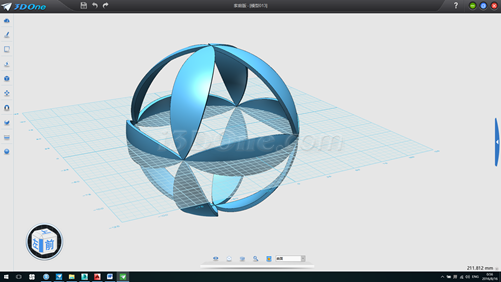
先看效果圖（圖案可以自己任意編排）

我們知道正立面體的各角點正好外接球體，并且正多面體各個面全等，看下圖

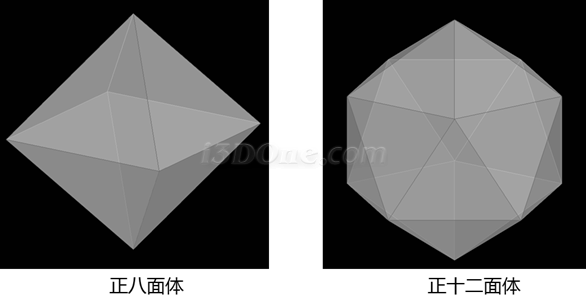
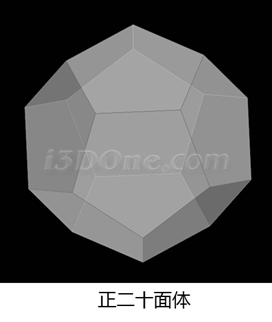
通過上面正立面體與球體的圖示，我們只要知道正立面體棱長與球體半徑的關系后，在正立面體各個面上繪制相應圖案后，利用3DOne軟件的投影曲線和曲面分割命令，將各個面上繪制的圖案投影到球體上，將不需要的面刪除，最后再利用抽殼命令即可生成立體等大圖案的模型。

因為正立面體和球體都是我們必須要的，正立面體的各個面便于我們繪制圖案，而球體是作為投影曲線用的，問題的重點是棱長已知，球體的半徑如何求？我們可以運用數學的知識的求解，但是在3DOne軟件中，這個問題很好解決，看下面所作輔助線。

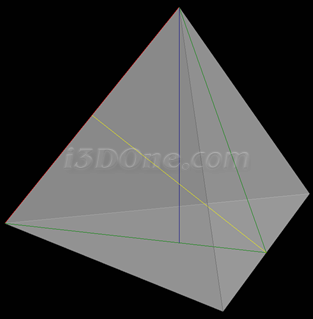
正四面體，藍線與黃線交點為球心，藍線上半部分為半徑，紅線為棱長

正六面體，綠線為球體直徑

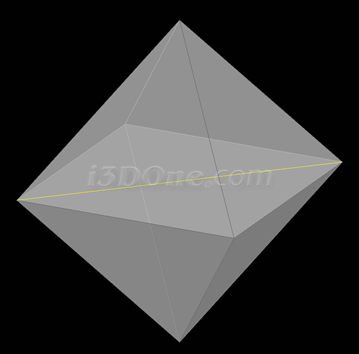
  正八面體，黃線為球體直徑

 

一、以正四面體為例看如何制作等大圖案的球體鏤空效果：

_ueditor_page_break_tag_

1.看上圖正四面體的輔助線，在3DOne中繪圖，先繪制邊長為100（此為紅線棱長長度）的正三角形，作出高線，高線即為上圖中綠線的長度（利用3DOne距離測量工具測得長度為86.60254，如下圖：

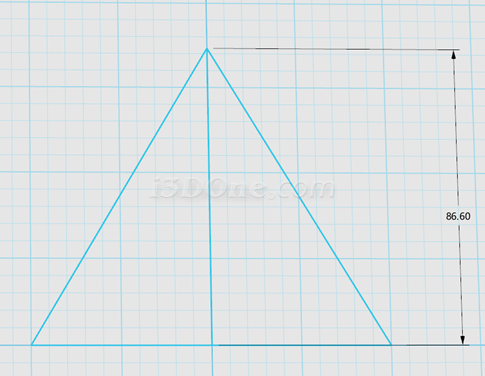
2.在旁邊繼續畫一水平線長度為86.60254，以直線兩端點分別畫半徑100和半徑86.60254兩個圓，如圖

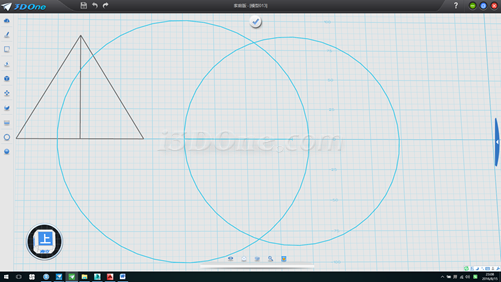
3.連接線段，并作出兩條高線，刪除兩輔助圓，如圖

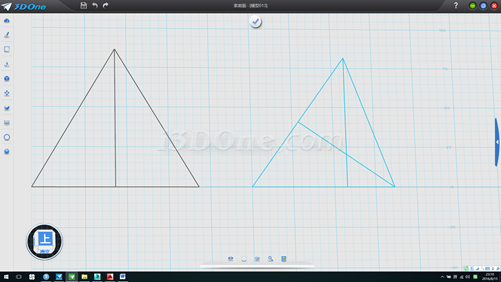
4.分別測得垂直高線的兩段長為61.2372（此為球半徑）和20.41241

5.刪除所有輔助線（為避免干攏后期作圖），畫100長直線，分別以兩端點畫半徑為100的圓，連接線段，如圖

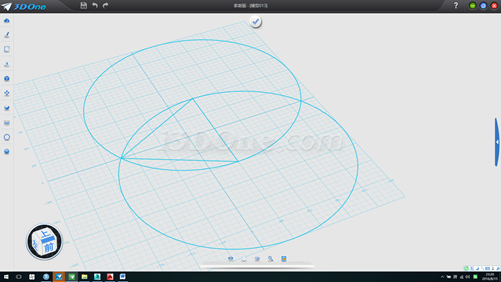
6.作兩高線，刪除輔助圓，將草圖兩高線交點處移至（0，0）點，如圖

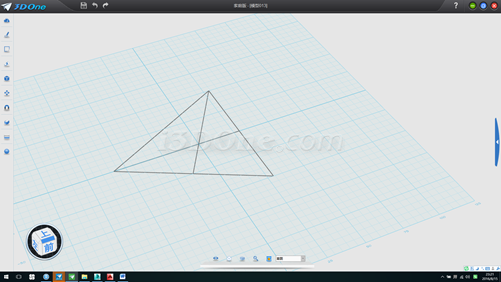
7.沿輔助線再描一邊長100的三角形并下移20.41241，如圖

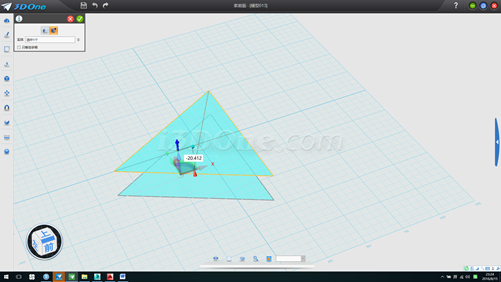
8.水平畫一長61.11056長的線段，旋轉90度，移動使下端點位于（0，0）處，如圖

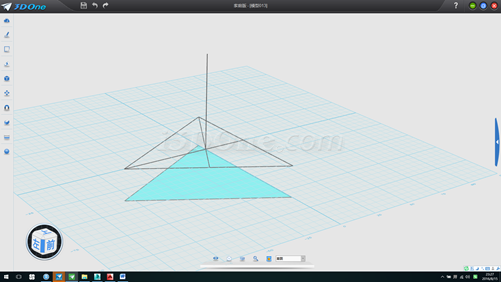
9.沿輔助圖形中一高線畫一直線（可畫長點以便于選擇）并向上拉伸一平面，如圖

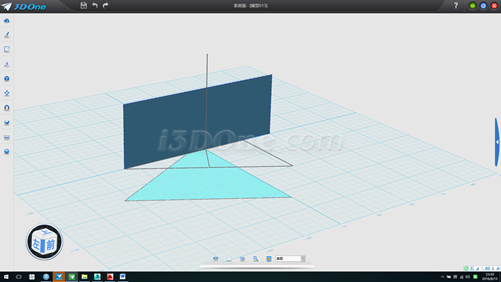
10.以此面為基準面畫直線連接兩線段端點，如圖：

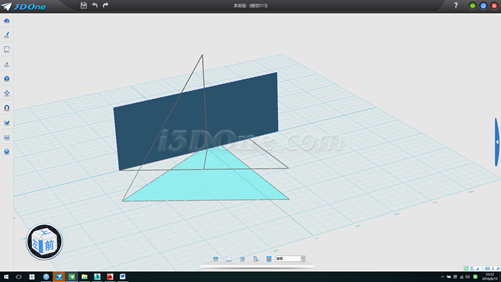
11.刪除輔助線和面，環形陣列剛畫的線，方向（0，0，1）數量3個，如圖

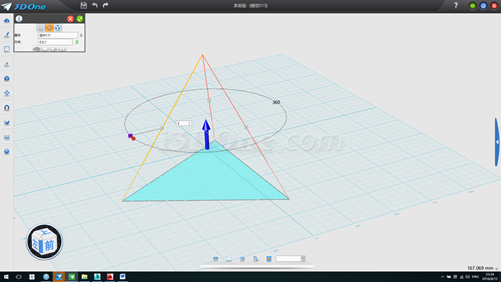
12.分別執行放樣命令（注意連續方式選擇無，如連續方式為灰色不可選則默認）四次即可求得正四面體形狀，且重心位于（0，0），（若底面不能放樣，則將底部三角形草圖刪除，以邊形式放樣即可）如圖：

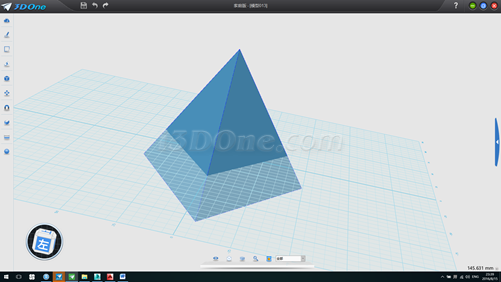
13.分別以兩個面為基準面繪制圖案，此例以畫一弧為例說明，如圖

_ueditor_page_break_tag_

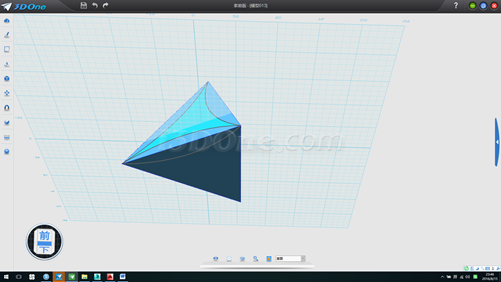
環形陣列，中心點(0,0,1)，數量3個，如圖

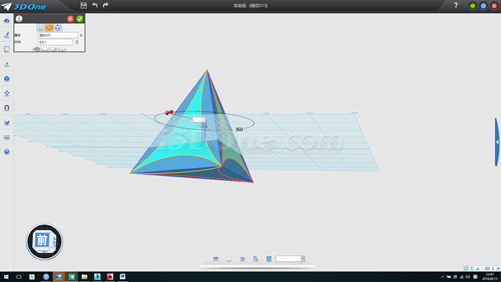
14.刪除四個輔助面，并以（0，0）為球心作半徑61.2372的球，將渲染模式設為線框模式（或者按CTRL+F）,如圖

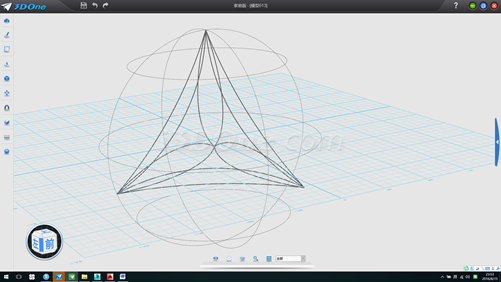
15.使用投影曲線命令將草圖投影 球表面，并使用曲面分割命令對球表面進行分割，如圖

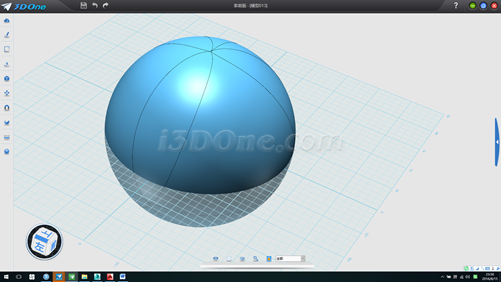
16.刪除不需要的面，使用抽殼命令給模型增加厚度，如圖

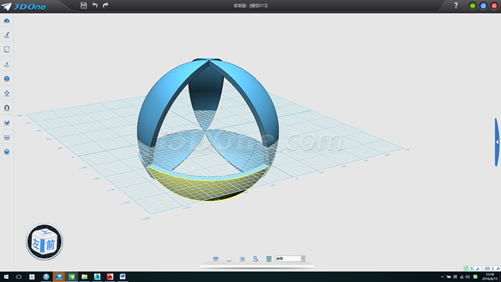
觀察一下，是不是每個形狀都是一樣大呢。

 

同理，正立面體做法如下：

1.以（0，0）畫長寬高分另為100的正方體，使用距離測量工具測得正方體兩對角點距離為173.2051,此為球體直徑長度，如圖

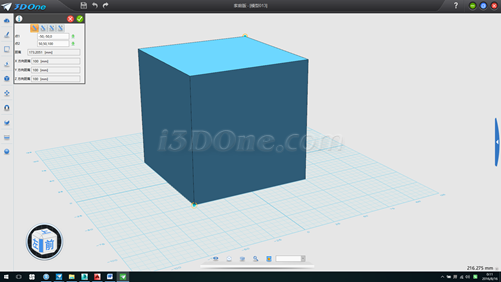
2.分別在六個面上繪制圖案如圖

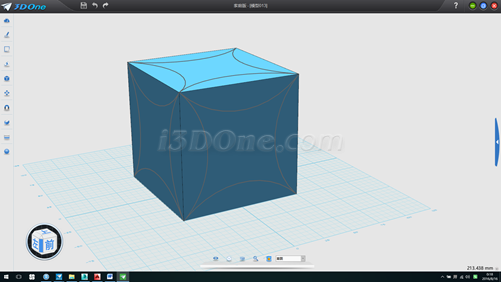
3.刪除六面體，以（0，50）為球心作半徑為86.60255為球體，后面的步驟同正四面體，最終效果如圖

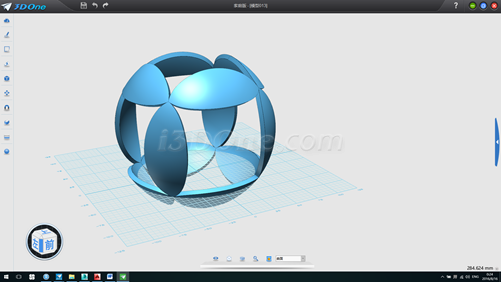
正八面體做法如下

1.畫邊長100的正方形，并將中心移至（0，0）退出草圖模式，如圖

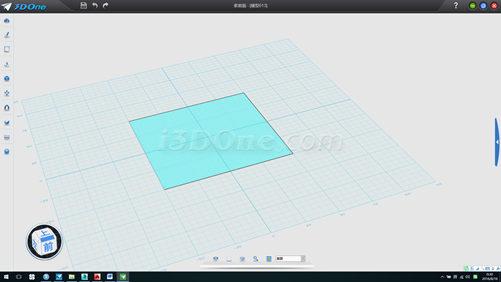
2.連接對角線(對角線一半長度70.71068即為球半徑)，刪除正方形，向上拉伸對角線高度100，并以此拉伸面為基準面分別在剛才對角線兩端點畫半徑100的圓，如圖

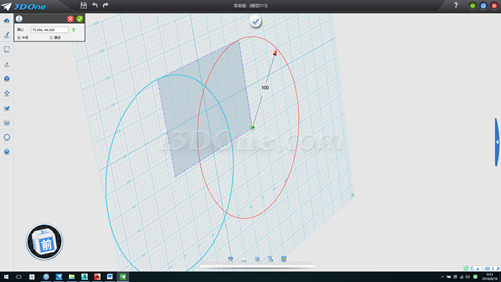
3.連接線段并刪除輔助圓，退出草圖模式，刪除基準面，如圖

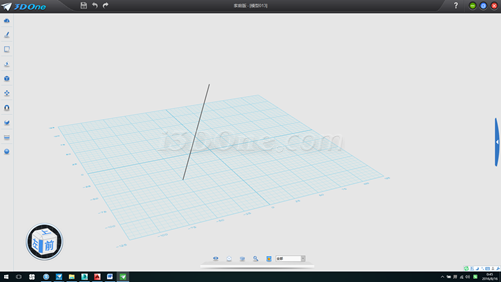
4.環形陣列，方向(0,0,1),數量4個，如圖

_ueditor_page_break_tag_

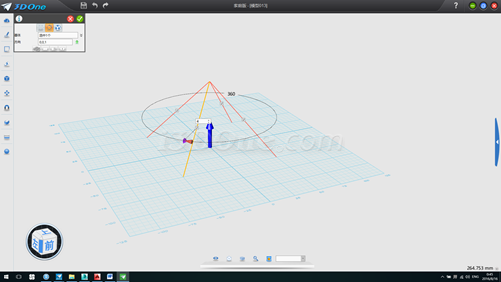
5.  再次環形陣型列，方向（1，0，0），數量2個，如圖

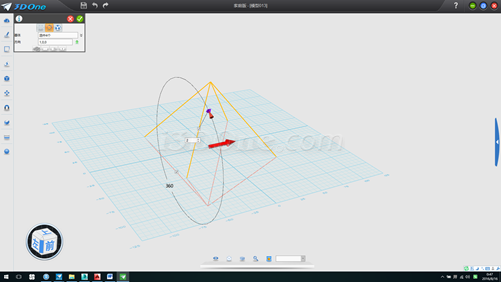
6.放樣，后面步驟同正四面體，最終效果如下：

正十二面體的做法復雜些（其中涉及數學知識我們不深入討論了）

1.先以（0，0）為圓心畫正五邊形，半徑為50，再畫另外兩個半徑50的五邊形，旋轉36度并移動至合適位置，如圖

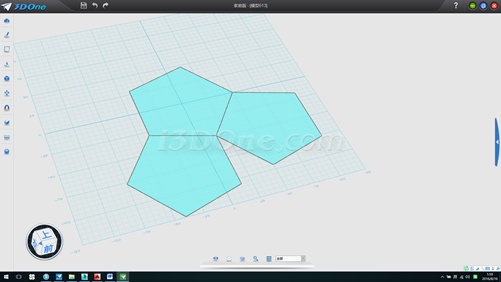
2.分別以兩個五邊形角點向另一五邊形的邊作垂線，如圖

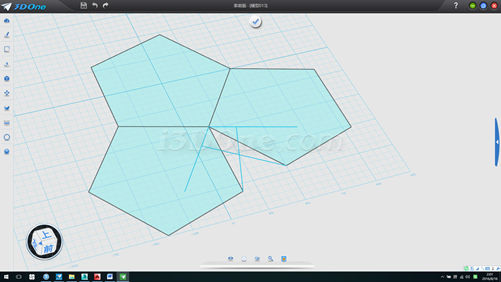
3.測得垂線長度55.9017，修剪，如圖

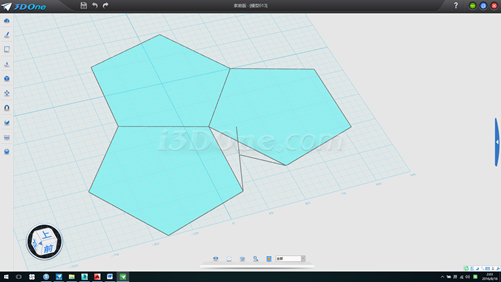
4.  拉伸所繪線高度100，以此拉伸面為基準面，以垂足點為圓心畫半徑55.9017的圓，以交點為起點向上畫一直線，如圖

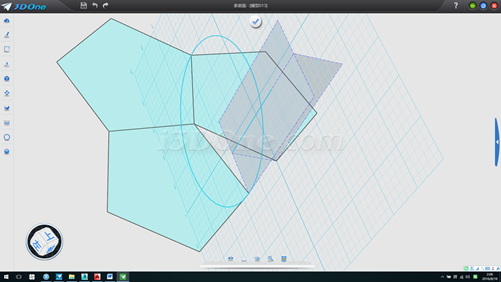
5.修剪線段冒頭部分，刪除圓和拉伸面，如圖

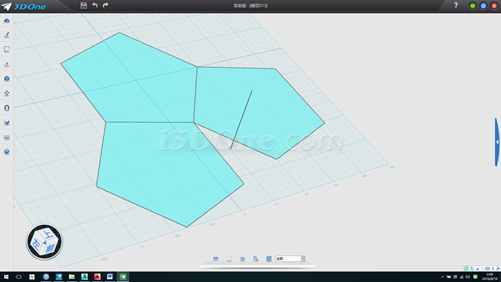
6.在平面上畫一線段，如圖

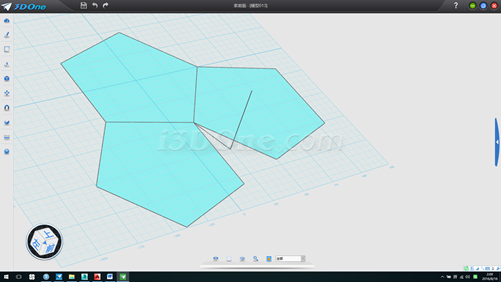
7.放樣，并以此放樣面為基準面畫一斜線（紅線位置），測得斜線長度58.77853，此為五邊形邊長的長度，如圖

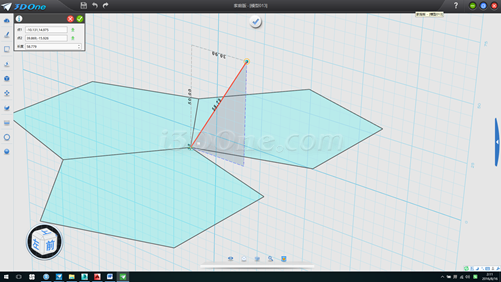
8.刪除基準面，環形陣列斜線2個，角度為-72度，方向（0，0，1）如圖

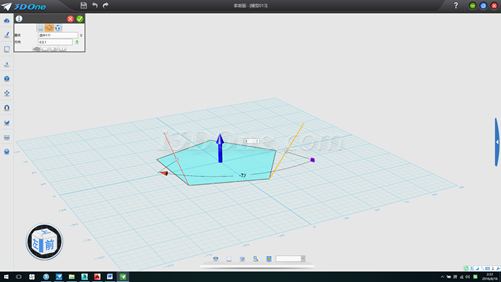
9.放樣兩根線作為基準面，以此基準面上兩個端點畫兩個半徑為58.77853的圓，如圖

_ueditor_page_break_tag_

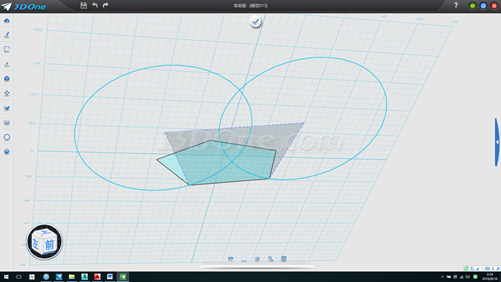
10.連五條線構成五邊形，刪除輔助圓和基準面，如圖

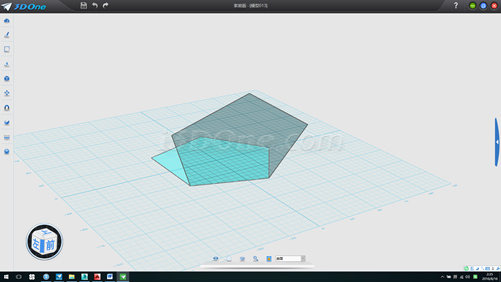
11.分別將兩五邊形向上向內拉伸若干，然后刪除多余面，如圖

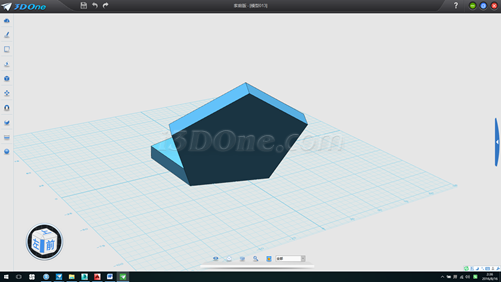
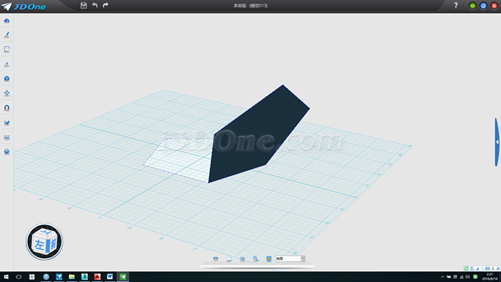
12.將斜平面環形陣型列五個，方向（0，0，1）角度360，如圖

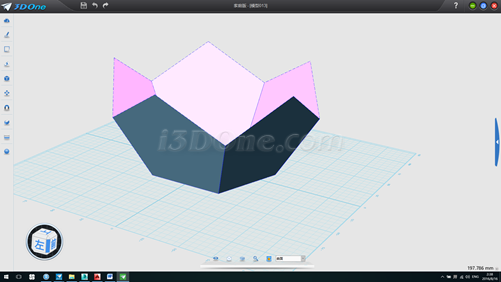
13.再次將六個物體環形陣列，方向（1，0，0），數量2個，如圖

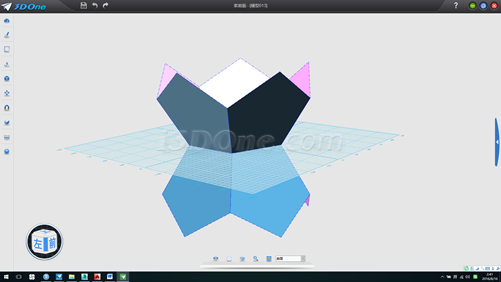
14.將陣列的六個上移，然后旋轉36度，再移至合適位置即可構成正十二面體，如圖

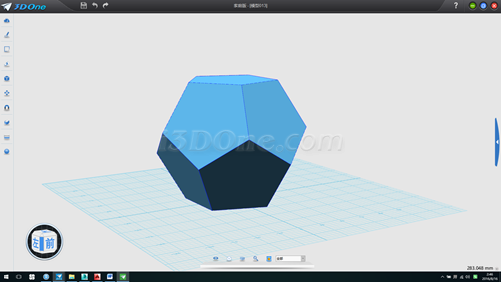
15.接下來我們找球心及球半徑，按CTRL+F轉線框模式，在最下方的五邊形內畫一條線，如圖

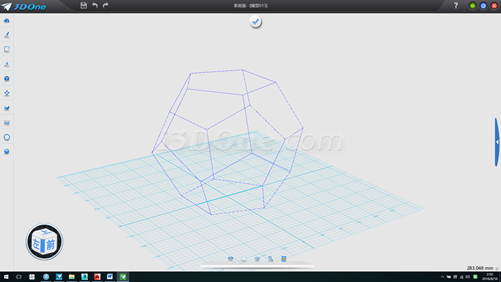
16.將此線向上拉伸高于整個多面體，并以此拉伸面作為基準面畫線連接圖上左右兩個頂點，此線即為球體直徑長度，測得直徑一半長度為82.36391，中心即為球心，如圖

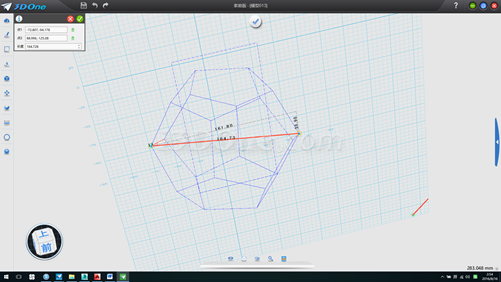
17.選擇所有物體，移動，以直線中心為起始點，目標點為（0，0），刪除直線和輔助面，如圖

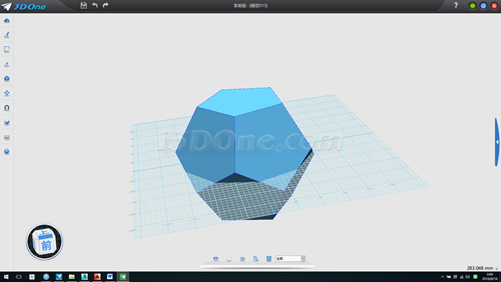
18.其他步驟同上，效果如下

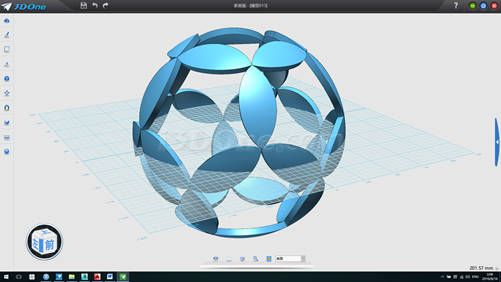
最后我們來看正二十面體是如何制作出來的

1.以（0，0）為圓心畫半徑50的正五邊形，距離測量邊長為58.77853，作輔助線，如圖

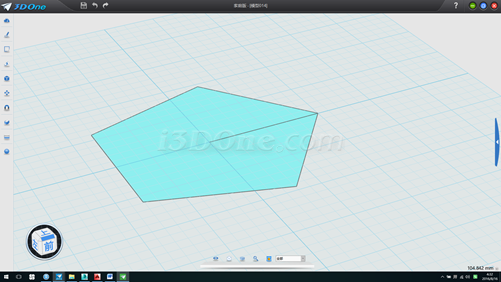
2.先隱藏五邊形，向上拉伸直線，以拉伸的面為基準面畫半徑為58.77853的圓和從（0，0）點向上畫一直線，如圖

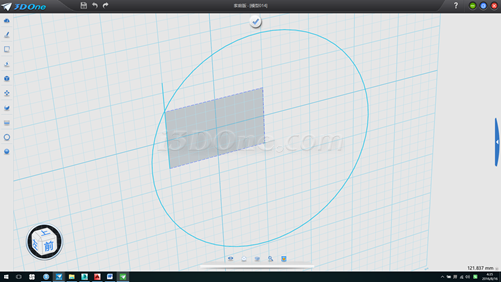
3.修剪直線，并刪除圓，如圖

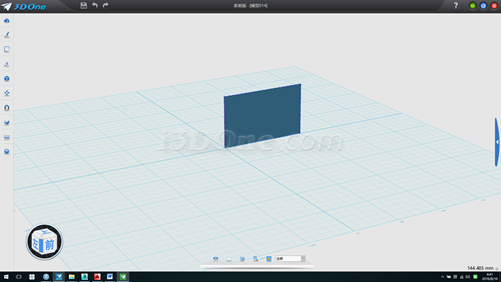
4.將隱藏物體顯示，放樣，放樣類型為起點到輪廓，連續方式為無，如圖

_ueditor_page_break_tag_

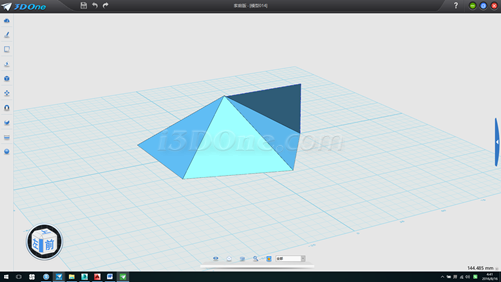
5.刪除底部平面，再以剛拉伸面為基準面，作輔助線，如圖

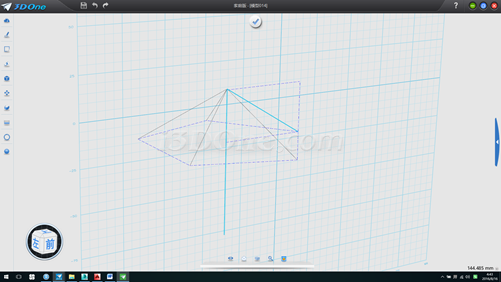
6.將斜線繞自身中心旋轉90度，并使用修剪、延伸曲線命令，然后再利用修剪命令修剪多余線段，如圖

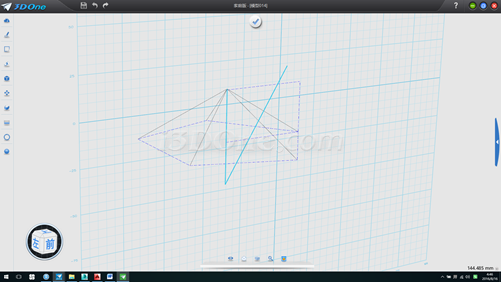
7.刪除斜線，垂線即為球的半徑，測得長度為55.90119，將拉伸面繞X軸旋轉90度，并移至垂線下端點對齊，將五面體以拉伸面為鏡像平面鏡像到下面，如圖

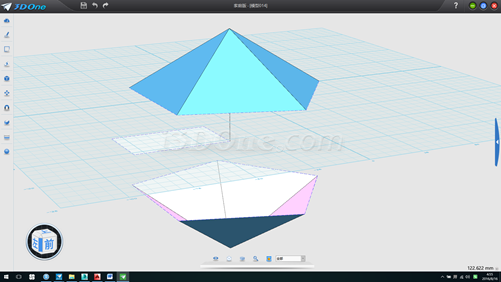
8.將上面五面體繞Z軸旋轉36度，并移動它使頂點與垂線頂點對齊，選擇所有物體，移動使垂線下端點作為起始點，目標點為（0，0），刪除拉伸面，如圖

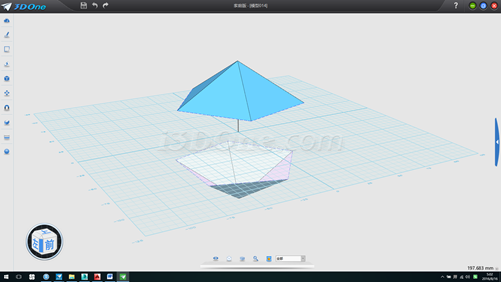
9.拉伸垂線，方向(1,0,0),如圖

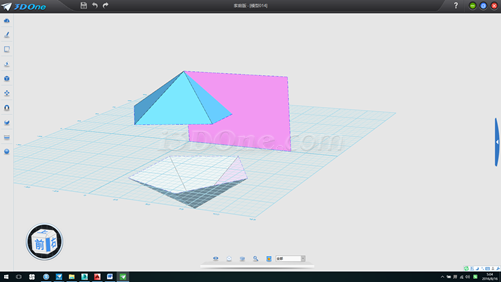
10.以此拉伸面為基準面，作輔助線，刪除輔助面，如圖

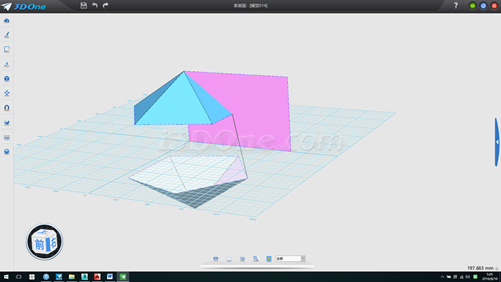
11.  拉伸輔助線，方向為上五面體的邊，如圖

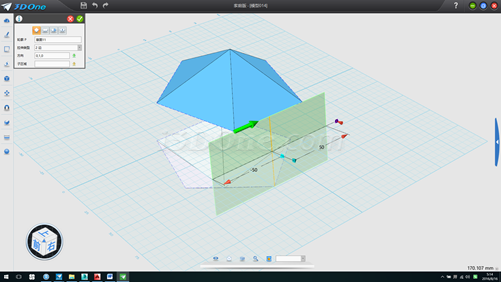
12.以此拉伸面為基準面分兩次畫兩線段，如圖

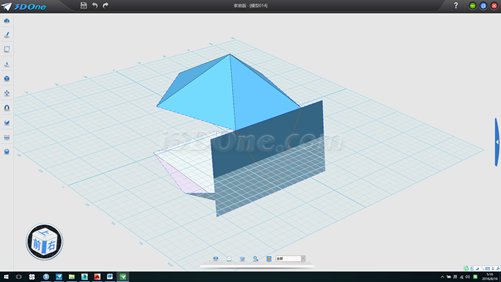
13.將拉伸面環形陣列，方向（0，0，1），數量2個，角度-72度，并以此拉伸面為基準面畫一條線段，如圖

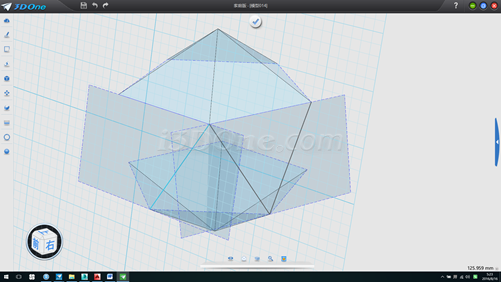
14.刪除兩基準面，分別放樣出兩個平面，注意放樣連續方式為無或默認不可選，如出現面反向（粉紅色表示）不影響，如圖

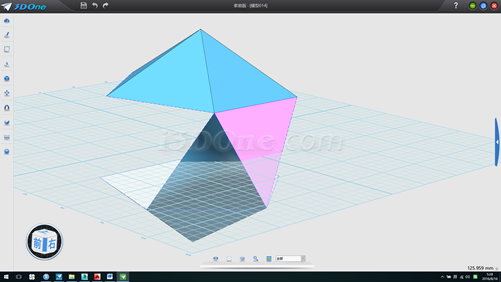
15.環形陣列兩個放樣面，方向（0，0，1）數量5個，角度360，如圖

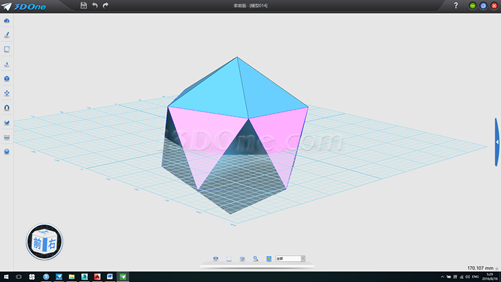
16.  其他步驟同上，效果如下

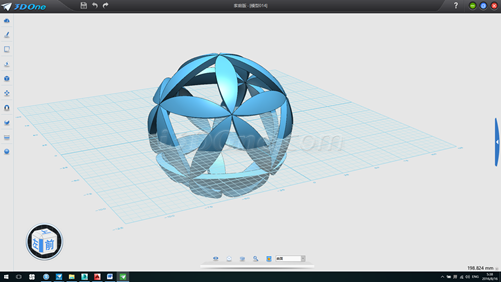
無論是利用正四面體還是正十二面體制作等大圖案的球形鏤空，原理都是一樣的。在建模過程中，動用數學的思維除了能夠幫助理解，還能起到事半功倍的效果。

點擊查看蘇文忠老師更多精彩教程